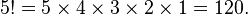A recursive function is a function that, at some point during it's execution, calls itself. This type of function can be very useful for iterating over data where the total number of elements/objects is not readily apparent, such as in a linked list; or branching is required to access all elements, as in an array whose elements may be arrays which may contain further arrays as elements. In this tutorial, we'll look closely at how recursive functions work over several examples.
A recursive function will typically first check if a condition is satisfied. This condition is called the base case. If the condition is met, the function will return a value or perform some other task. If the condition is not met, the function will return a call to itself with modified arguments. This cycle will continue until the condition is met, returning any target value back through the stack to the initial call.
Example 1 - Searching a linked list
function searchList(list, named){
if (list == null){return 'Not Found';}
if (list.name == named){
return list.status;
} else {
return searchList(list.next, named);
}
}
var sunnyVale = {name: 'Ricky',
status: 'Resident',
next: {name: 'Bubbles',
status: 'Resident',
next: {name: 'Julian',
status: 'Resident',
next: {name: 'Lahey',
status: 'Park Supervisor',
next: {name: 'Randy',
status: 'Assistant Park Supervisor',
next: null}}}}};
searchList(sunnyVale, 'Lahey'); //returns 'Park Supervisor'
searchList(sunnyVale, 'Randy'); //returns 'Assistant Park Supervisor'
searchList(sunnyVale, 'Julian'); //returns 'Resident'
searchList(sunnyVale, 'Bubbs'); //returns 'Not Found'In the example above, the function searchList takes 2 arguments, a linked list called list; and a string called named. searchList first checks if list is null (which would mean we have come to the end of the list) and returns 'Not Found' if so. The function then checks if the list property name equals the variable named we are looking for. If list.name matches named, then the value of list.status is returned. If not, searchList calls itself with list.next as the list to check. This continues like a loop until the right name is found, or the list ends.
function sum(num, add){
if (add===0){return num}
else {
num += 1;
return sum(num, add-1)
}
}
sum(9,10); //returns 19In this example, function sum adds two numbers. It does this by adding 1 to num and returning a call to sum with the argument add decremented by 1. When add is 0, num (having been incremented by 1 add number of times) is returned.
function factorial(n){
if (n==0 || n==1){
return 1;
}
return factorial(n-1)*n;
}
factorial(2) // return 2A factorial number is defined as follows:
In this example, the base case is n = 1. n = 0 is added as alternative to take into account the value zero as input.
When the function is invoked, for example with the value 2 as input, one instance of the function is added to the execution stack. Since n is not equal to the base case, the function calls itself again, this time with the input value of n-1, which is one. The first created instance of the function remains in the execution stack as it waits for the second instance to return a value. In the second instance of the function the base case is met, and one is returned to the first instance. The value is multiplied by the value of n inside the first instance, so 1*2, and then returned. The result, as expected, is 2.
This is a classic example used for recursion, as there is a significant advantage in calculating a factorial in this way, in terms of simplicity of code. Try to solve the same problem using a for loop to see for yourself.
A common problem found in many Codewars kata is how to generate the Fibonacci sequence. The first two numbers in the Fibonacci sequence are either 1 and 1, or 0 and 1 and each subsequent number is the sum of the previous two.
The first method we’re going to look at is by looping since it is often easier for people to wrap their head around.
var looping = function(n) {
var a = 0, b = 1, f = 1;
for(var i = 2; i <= n; i++) {
f = a + b;
a = b;
b = f;
}
return f;
};We know that each Fibonacci number is the sum of the previous two sequence numbers, which is why we are starting our loop at index two, which is really the third value since our index starts at zero. The first two numbers in our sequence are zero and one. The goal is to find the Fibonacci number at a certain sequence index, which in this example is fifteen.
Every loop iteration we are summing the previous two sequence values, then pushing our values up, in a sense. By this I mean that a is dropped off and replaced with b and b is replaced with the current index value of the sequence, being our new sum. When our loop has reached our desired fifteen index, we can return whatever the new sum value is.
Now let’s take a look at the recursive version of this.
var recursive = function(n) {
if(n <= 2) {
return 1;
} else {
return recursive(n - 1) + recursive(n - 2);
}
};Recursion can be a little tricky to wrap your head around. In the above code, we are going to plan on receiving the sequence value at index five because anything larger is going to be rough for me to type out. You can break this down like the following:
recursive(4) + recursive(3)
(recursive(3) + recursive(2)) + (recursive(2) + recursive(1))
((recursive(2) + recursive(1)) + 1) + (1 + 1)
((1 + 1) + 1) + (1 + 1)
5You can see above that on every line the function is one further iteration through the recursive process. Based on our function logic, as soon as n <= 2 then we just return a value of one. At the furthest breakdown, our sum turns into five which is the Fibonacci number at index five.
Example Kata -> Fibonacci Reloaded & Complete Fibonacci Series.
Recursive functions have two main drawbacks. One is that repeatedly calling a function is less efficient when a standard for or while loop will do the job. The other is that each recursive call adds another function to the stack, consuming more and more memory each time. Calling sum from Example 2 like this: sum(9,100000); would result in a 'Range' or 'Too much recursion' error as the stack would overflow.
Consult the links below for a tutorial on Tail Call Optimisation for further information.
##Related