We run a preorder depth first search on the root of a binary tree.
At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. (If the depth of a node is D, the depth of its immediate child is D+1. The depth of the root node is 0.)
If a node has only one child, that child is guaranteed to be the left child.
Given the output S of this traversal, recover the tree and return its root.
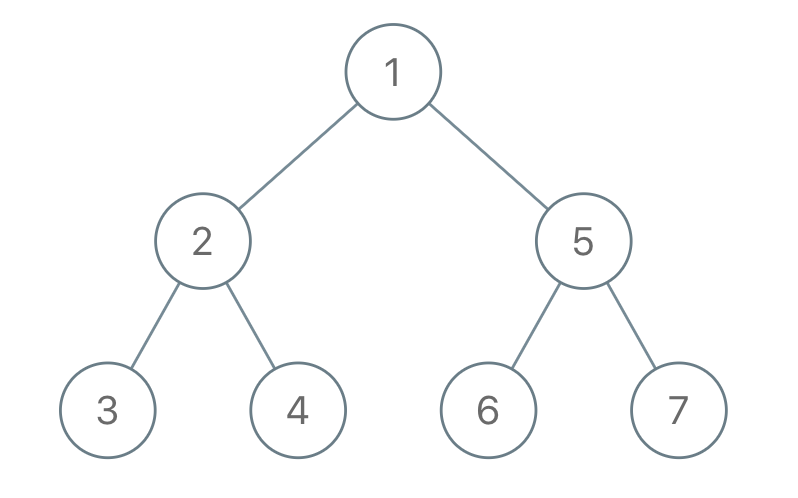
Input: "1-2--3--4-5--6--7" Output: [1,2,5,3,4,6,7]
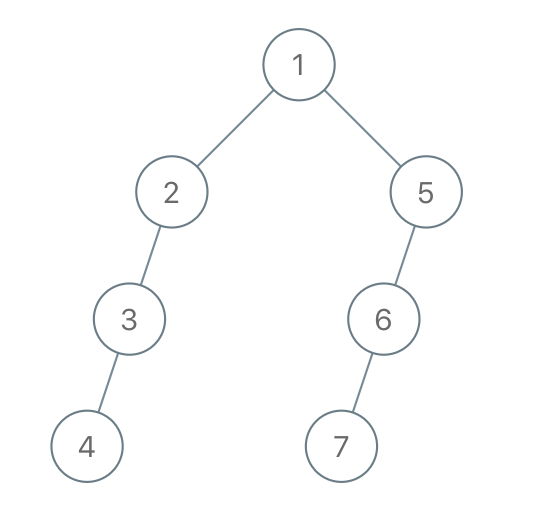
Input: "1-2--3---4-5--6---7" Output: [1,2,5,3,null,6,null,4,null,7]
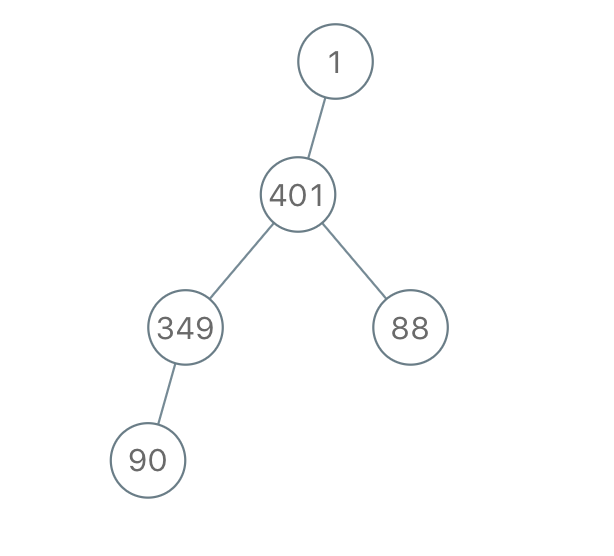
Input: "1-401--349---90--88" Output: [1,401,null,349,88,90]
- The number of nodes in the original tree is between
1and1000. - Each node will have a value between
1and10^9.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def recoverFromPreorder(self, S: str) -> TreeNode:
vals = [int(n) for n in S.split('-') if n != '']
depths = [0]
depth = 0
for ch in S:
if ch == '-':
depth += 1
elif depth != 0:
depths.append(depth)
depth = 0
stack = []
while vals:
node = TreeNode(vals.pop(0))
depth = depths.pop(0)
while stack and stack[-1][1] >= depth:
stack.pop()
if stack and not stack[-1][0].left:
stack[-1][0].left = node
elif stack and not stack[-1][0].right:
stack[-1][0].right = node
stack.append((node, depth))
return stack[0][0]