README.md

2579. Count Total Number of Colored Cells

There exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer n, indicating that you must do the following routine for n minutes:

• At the first minute, color any arbitrary unit cell blue.
• Every minute thereafter, color blue every uncolored cell that touches a blue cell.

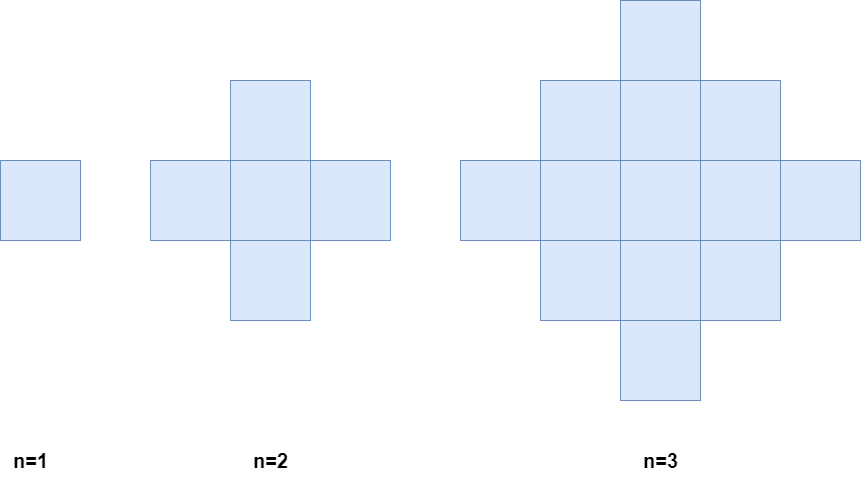
Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.

Return the number of colored cells at the end of n minutes.

Example 1:

Input: n = 1
Output: 1
Explanation: After 1 minute, there is only 1 blue cell, so we return 1.

Example 2:

Input: n = 2
Output: 5
Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5.

Constraints:

• 1 <= n <= 105

Solutions (Rust)

1. Solution

impl Solution {
    pub fn colored_cells(n: i32) -> i64 {
        (1..n as i64).fold(1, |acc, x| acc + x * 4)
    }
}