-
Notifications
You must be signed in to change notification settings - Fork 0
5. Post Hoc tests
For the purposes of this document we will continue with the following:
base_model <- MCMmodel(data_summary, n_latent=2, constrained_a=FALSE)
no_A_model <- MCMedit(base_model, "A", "a", 0)
coords <- expand.grid(x=1:5+2, y=1:5+2)[upper.tri(matrix(0, 5, 5), diag=FALSE), ]
unidirectional_model <- MCMedit(base_model, pointer="A", name=list(coords$x, coords$y), value=0)
base_result <- MCMfit(base_model, data_summary, optim_iters=c(500, 25), monitor_grads=TRUE)
no_A_result <- MCMfit(no_A_model, data_summary, optim_iters=c(500, 25), monitor_grads=TRUE)
unid_result <- MCMfit(unidirectional_model, data_summary, optim_iters=c(500, 25), monitor_grads=TRUE)
As far as indicators of if the optimization is even working, checking if the loss decreases over iterations is the simplest one. Since the loss history is stored in the MCM result object as a vector, we can do this using the built-in plot() function.
par(mfrow=c(3, 1))
plot(base_result$history$loss, type='l', xlab='iteration', ylab='loss', main='base_result', ylim=c(0, 50))
plot(no_A_result$history$loss, type='l', xlab='iteration', ylab='loss', main='no_A_result', ylim=c(0, 50))
plot(unid_result$history$loss, type='l', xlab='iteration', ylab='loss', main='unid_result', ylim=c(0, 50))
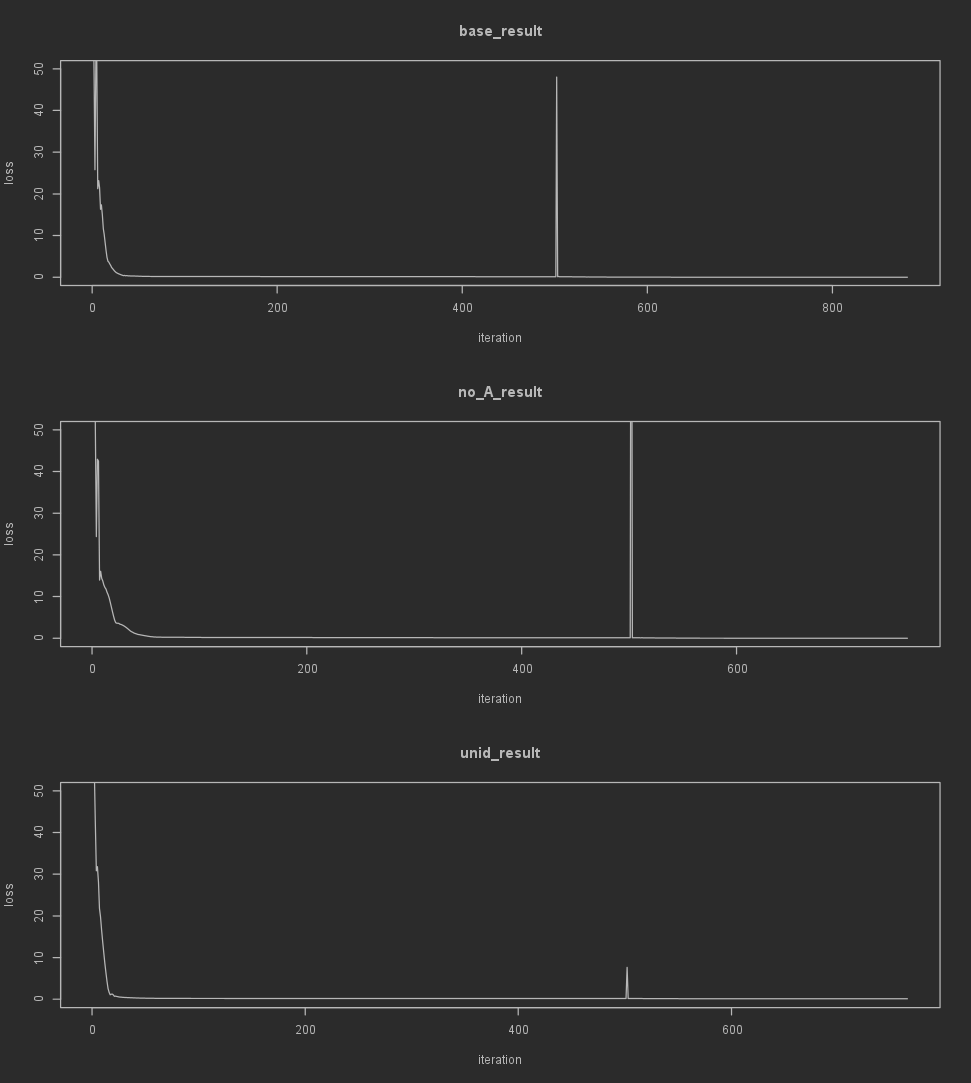
Note that when using different optimizers in sequence (especially with LBFGS) you'll likely see a peak in this graph when the next optimizers is initiated.
Additionally, we can look at the history of the gradients for each parameter. The gradients are included in the MCM result object as a custom class. This is mainly to make plotting and transforming the gradients easier. To obtain the full gradient history as a dataframe, to analyze it manually you can run the following:
base_result_grad_history_df <- as.data.frame(base_result$gradients)
To visualize all gradient histories we can run the following.
plot(base_result$gradients)
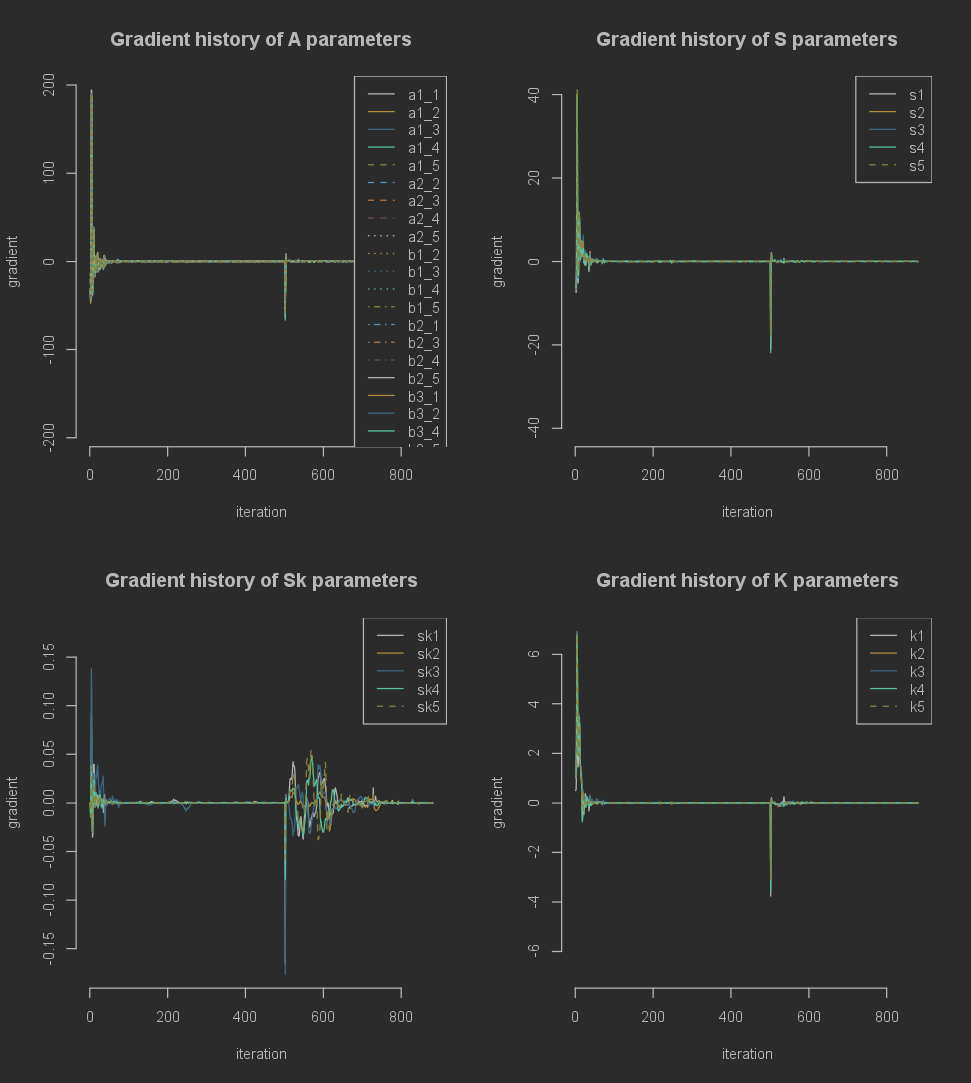
This splits the parameters into categories depending on which base matrix (see wiki pages on the MCM model) they originate from. Any additional arguments passed to this plot function will be applied to all subplots.
Alternatively you can zoom in on a single matrix.
plot(base_result$gradients$A)
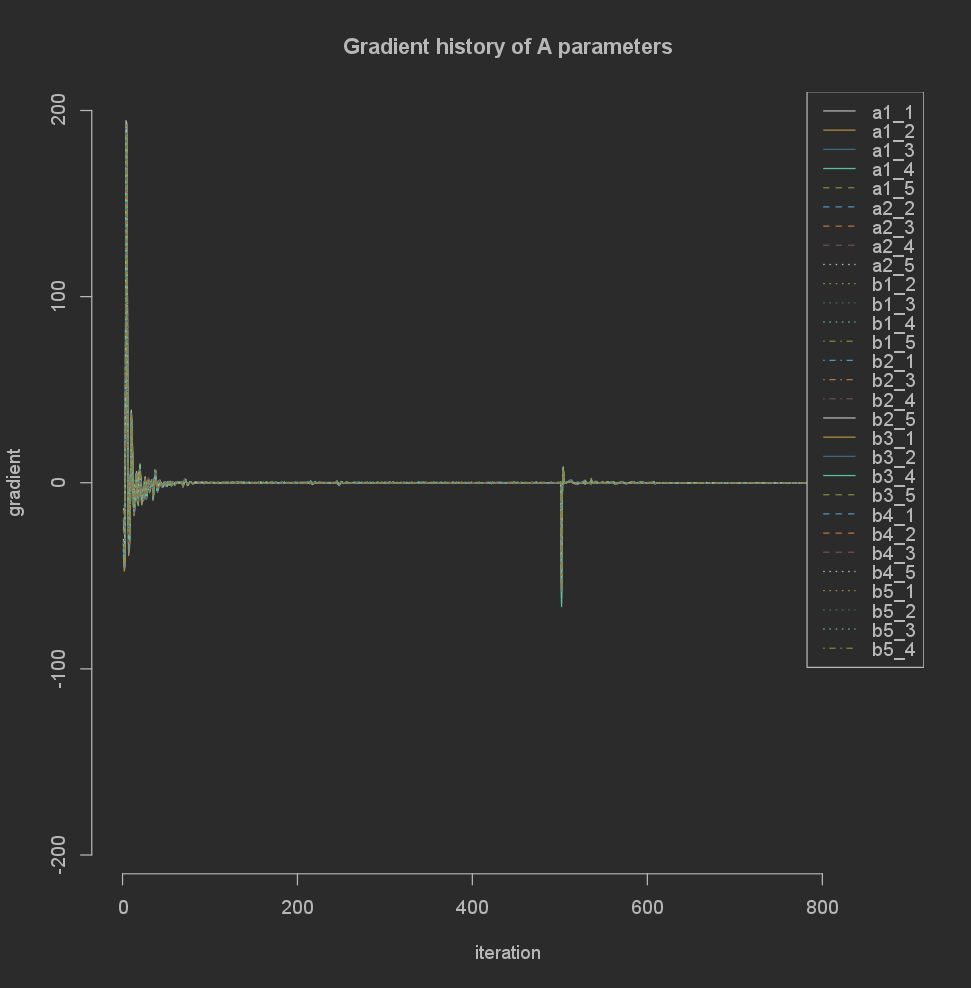
There are several options for scaling built in to the gradient classes, such as log, abs, and sqrt:
plot(sqrt(abs(base_result$gradients$A)))
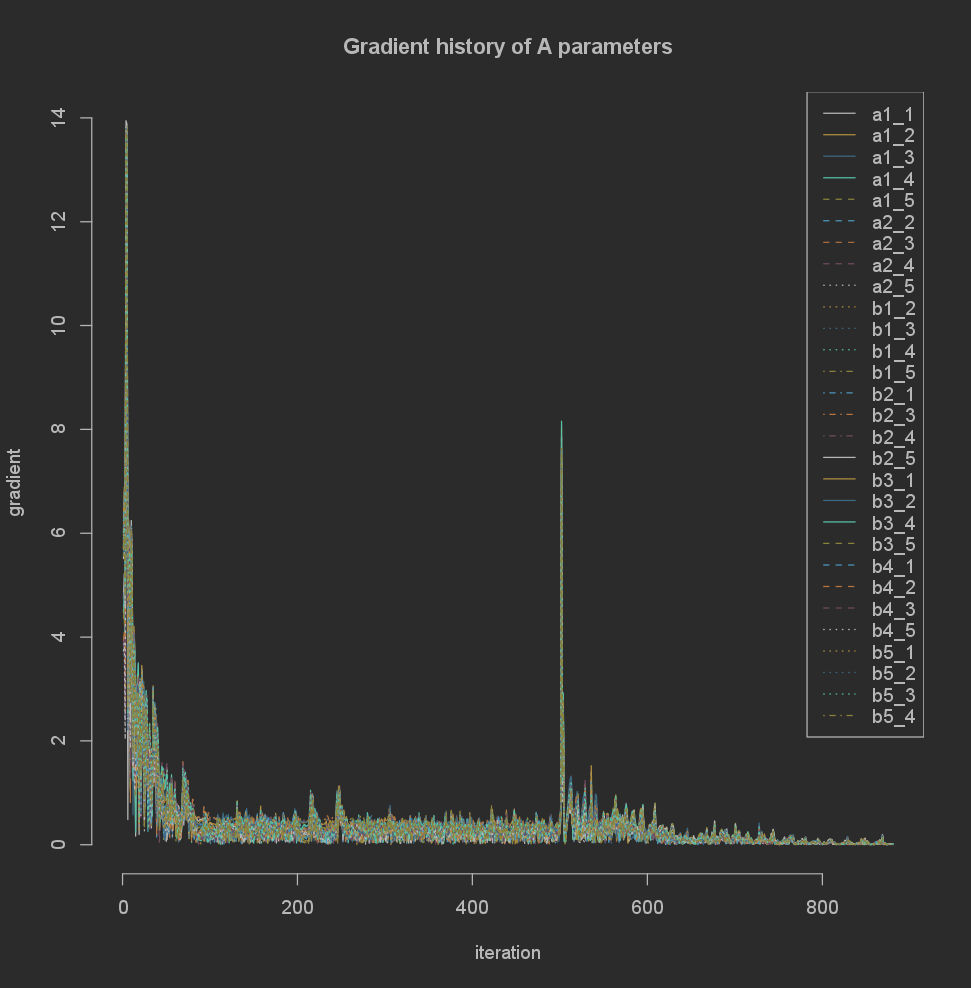
Finally, there are different summarizing methods for the gradient: min, max and summary. For example:
summary(base_result$gradients)
Will return a dataframe with a detailed summary with minimum, maximum of all values and absolute values, as well as gradient at the last iteration:
A.a1_1 A.a1_2 A.a1_3 A.a1_4 A.a1_5 A.a2_2 A.a2_3 A.a2_4 A.a2_5 A.b1_2 A.b1_3 A.b1_4 A.b1_5
min -5.143213e+01 -4.752067e+01 -4.420788e+01 -5.223549e+01 -4.621045e+01 -3.466873e+01 -3.283141e+01 -3.769374e+01 -3.238495e+01 -5.587294e+01 -5.091473e+01 -6.167405e+01 -5.389321e+01
max 7.585236e+01 1.124280e+02 1.104663e+02 1.113398e+02 1.149420e+02 1.003268e+02 9.872623e+01 9.929739e+01 1.020223e+02 1.412878e+02 1.383869e+02 1.388800e+02 1.453401e+02
min(abs) 5.621114e-06 1.659617e-06 1.322373e-05 1.165841e-06 5.611684e-06 1.711422e-06 4.531583e-06 1.022825e-05 1.128111e-05 9.220093e-07 1.654774e-05 2.295338e-05 1.657475e-05
max(abs) 7.585236e+01 1.124280e+02 1.104663e+02 1.113398e+02 1.149420e+02 1.003268e+02 9.872623e+01 9.929739e+01 1.020223e+02 1.412878e+02 1.383869e+02 1.388800e+02 1.453401e+02
last iteration -1.108114e-04 -1.287877e-04 -1.134933e-04 -1.587445e-04 -2.443558e-04 -6.612344e-05 -3.770762e-05 -1.013982e-04 -6.455206e-05 -2.995590e-04 -2.861554e-04 -3.193808e-04 -4.322873e-04
A.b2_1 A.b2_3 A.b2_4 A.b2_5 A.b3_1 A.b3_2 A.b3_4 A.b3_5 A.b4_1 A.b4_2 A.b4_3 A.b4_5 A.b5_1
min -6.176170e+01 -5.437886e+01 -6.540476e+01 -5.780648e+01 -6.431362e+01 -6.057674e+01 -6.656063e+01 -5.829870e+01 -5.806892e+01 -5.388167e+01 -5.221352e+01 -5.407223e+01 -5.598459e+01
max 1.210252e+02 1.862775e+02 1.877108e+02 1.945052e+02 1.200645e+02 1.887515e+02 1.855341e+02 1.925772e+02 1.185707e+02 1.872007e+02 1.829224e+02 1.912507e+02 1.222052e+02
min(abs) 2.282555e-06 7.185154e-06 5.502952e-06 1.378357e-07 1.078937e-05 1.328066e-06 5.343370e-05 1.764297e-05 2.306886e-06 4.621223e-06 1.463736e-05 1.746509e-05 8.797739e-06
max(abs) 1.210252e+02 1.862775e+02 1.877108e+02 1.945052e+02 1.200645e+02 1.887515e+02 1.855341e+02 1.925772e+02 1.185707e+02 1.872007e+02 1.829224e+02 1.912507e+02 1.222052e+02
last iteration -2.667808e-04 -2.801595e-04 -3.738813e-04 -4.841434e-04 -3.154050e-04 -3.559701e-04 -3.840011e-04 -4.847776e-04 -2.578460e-04 -3.270321e-04 -2.933447e-04 -4.476309e-04 -2.627824e-04
A.b5_2 A.b5_3 A.b5_4 S.s1 S.s2 S.s3 S.s4 S.s5 Sk.sk1 Sk.sk2 Sk.sk3 Sk.sk4 Sk.sk5
min -5.305309e+01 -5.121470e+01 -5.828861e+01 -2.115492e+01 -1.994950e+01 -1.962381e+01 -2.188124e+01 -1.790882e+01 -1.652053e-01 -2.363268e-02 -1.765271e-01 -7.858545e-02 -5.690962e-02
max 1.905715e+02 1.865612e+02 1.879217e+02 2.245840e+01 4.006755e+01 3.923344e+01 3.959208e+01 4.115178e+01 9.197994e-02 2.892910e-02 1.378856e-01 4.837161e-02 5.425204e-02
min(abs) 1.340220e-05 1.281477e-05 3.486872e-06 1.545064e-06 1.387671e-07 7.711351e-07 2.146699e-07 2.179295e-06 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
max(abs) 1.905715e+02 1.865612e+02 1.879217e+02 2.245840e+01 4.006755e+01 3.923344e+01 3.959208e+01 4.115178e+01 1.652053e-01 2.892910e-02 1.765271e-01 7.858545e-02 5.690962e-02
last iteration -3.279084e-04 -3.006561e-04 -3.196449e-04 -6.734114e-05 -9.906944e-05 -7.002614e-05 -8.970825e-05 -1.141196e-04 9.421608e-06 -2.770525e-06 -8.193325e-06 1.694891e-06 1.165568e-05
K.k1 K.k2 K.k3 K.k4 K.k5
min -3.764635e+00 -3.166836e+00 -3.313023e+00 -3.622292e+00 -3.098831e+00
max 4.212971e+00 6.899916e+00 6.926666e+00 6.746869e+00 6.816867e+00
min(abs) 1.102453e-07 4.834263e-06 5.845213e-07 5.410402e-07 4.575806e-06
max(abs) 4.212971e+00 6.899916e+00 6.926666e+00 6.746869e+00 6.816867e+00
last iteration 1.102453e-07 -4.247428e-05 -2.113427e-05 3.863533e-06 1.728674e-05
Finally, when you have fitted different models, you can compare their performance in terms of loss calculated from a dataset (ideally a seperate holdout dataset) using the MCMcompareloss() function.
The input to this function should be a list of MCM result objects (names of the list will be used as rownames in the output), and the MCM data summary of the holdout sample:
MCMcompareloss(list(Base=base_result, NoA=no_A_result, Unidir=unid_result), holdout_summary)
This will return a dataframe detailing the loss, chisq and bic in both the training dataset and the holdout (test) dataset, as well as the difference in loss, and the number of parameters of each model
mse_train_loss train_chisq train_bic mse_test_loss mse_diff mse_test_chisq mse_test_bic N_parameters
Base 0.002169265 54.23164 499.8034 0.3136756 NA 3136.756 3542.011 44
NoA 0.003176718 79.41796 433.8500 0.3139555 -0.0002798736 3139.555 3461.917 35
Unidir 0.118693106 2967.32765 3311.6331 0.4421709 -0.1284953058 4421.709 4734.861 34
For more extensive information about the models and results you can include extensive_model_info=TRUE
MCMcompareloss(list(Base=base_result, NoA=no_A_result, Unidir=unid_result), holdout_summary, extensive_model_info=TRUE)
Which will return the following
mse_train_loss train_chisq train_bic mse_test_loss mse_diff mse_test_chisq mse_test_bic N_parameters loss_type use_skewness use_kurtosis optim1 optim1_iters optim1_lr
Base 0.002169265 54.23164 499.8034 0.3136756 NA 3136.756 3542.011 44 mse TRUE TRUE rprop 500 0.02
NoA 0.003176718 79.41796 433.8500 0.3139555 -0.0002798736 3139.555 3461.917 35 mse TRUE TRUE rprop 500 0.02
Unidir 0.118693106 2967.32765 3311.6331 0.4421709 -0.1284953058 4421.709 4734.861 34 mse TRUE TRUE rprop 500 0.02
optim2 optim2_iters optim2_lr train_n version use_bounds compute_se se_type device low_memory Preparation_runtime Optimizer_runtime SE_runtime Total_runtime
Base lbfgs 25 1 25000 0.25.0 TRUE TRUE asymptotic cpu FALSE 0.05799985 42.4485 0.3590002 42.8655
NoA lbfgs 25 1 25000 0.25.0 TRUE TRUE asymptotic cpu FALSE 0.26200008 33.7770 0.3314979 34.3705
Unidir lbfgs 25 1 25000 0.25.0 TRUE TRUE asymptotic cpu FALSE 0.05549908 35.2225 0.2410011 35.5190