- 算法基础
- 时间复杂度
- 排序算法
- 数据结构
- 递归公式
- 主定理
- 表达式
- 链表
- 单向链表
- 双向链表
- 二叉树
- 类型
- 遍历方式
- 位运算
- 待定
- 图论
- 基础
- BFS
- DFS
- 算法对比
- 参考资料
- Algorithms and Data Structures Cheatsheet
| 类型 | 表达式 | 例子 | 代码示例 |
|---|---|---|---|
| 常数 | O(1) |
|
add() |
| 对数 | O(logn) |
|
for (i = 1 to Array.length, i = 2*i) |
| 线性 | O(n) |
|
for (i = 1 to Array.length, i += 1) |
| 线性方程 | O(nlogn) |
|
for (i = 1 to Array.length, i += 1) |
| 二次方 | O(n^2) |
|
for (i = 1 to Array.length, i += 1) |
| 多项式 | O(n^c) |
|
for (i = 1 to Array.length, i += 1) |
| 指数 | O(2^n) |
|
func recursion() |
| 类型 | 最好时间 | 平均时间 | 最坏时间 | 空间 | 稳定性 |
|---|---|---|---|---|---|
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 桶排序 | O(n) | O(n) | O(n^2) | O(n) | 稳定 |
| 类型(平均) | 获取元素 | 查找元素 | 插入元素 |
|---|---|---|---|
| 数组 | O(1) | O(n) | O(n) |
| 链表 | O(n) | O(n) | O(1) |
| 双向链表 | O(n) | O(n) | O(1) |
| 栈 | O(1) | O(n) | O(1) |
| 堆 | O(1) | O(n) | O(logn) |
| 队列 | O(1) | O(n) | O(1) |
| 哈希表 | O(1) | O(1) | O(1) |
| 二叉搜索树 | O(logn) | O(logn) | O(logn) |
| 跳表 | O(logn) | O(logn) | O(logn) |
| 类型 | T(n) | 例子 |
|---|---|---|
| T(n)=T(n/2)+1 | O(logn) | 二分查找 |
| T(n)=2T(n/2)+1 | O(n) | 二叉树遍历 |
| T(n)=2T(n/2)+n | O(nlogn) | 归并排序 |
| T(n)=T(n−1)+n | O(n^2) | 插入排序 |
| T(n)=2T(n−1)+1 | O(2^n) | 回溯算法 |
当 a≥1, b≥2, c>0 且 T(n) 在非负区间内满足 T(n) = aT(n/b)+O(nc),假定 T(0)=0,T(1)=O(1),则
| 类型 | T(n) |
|---|---|
| c<log(b)a | O(n * log(b)a) |
| c=log(b)a | O(n^c * logn) |
| c>log(b)a | O(n^c) |
| 类型 | 表达式 | 结果 |
|---|---|---|
| 调和级数 | 1+1/2+1/3+…+1/n | log(e)n |
| 自然对数 | (1+1/n)^n | e |
| 等差数列 | n1+n2+n3+n4..n | n(n1+n)/2 |
| 等比数列 | n1+n2+n3+n4..n | n1(1-q^n)/(1-q) |
| 卡特兰数 |
| 类型 | 简介 |
|---|---|
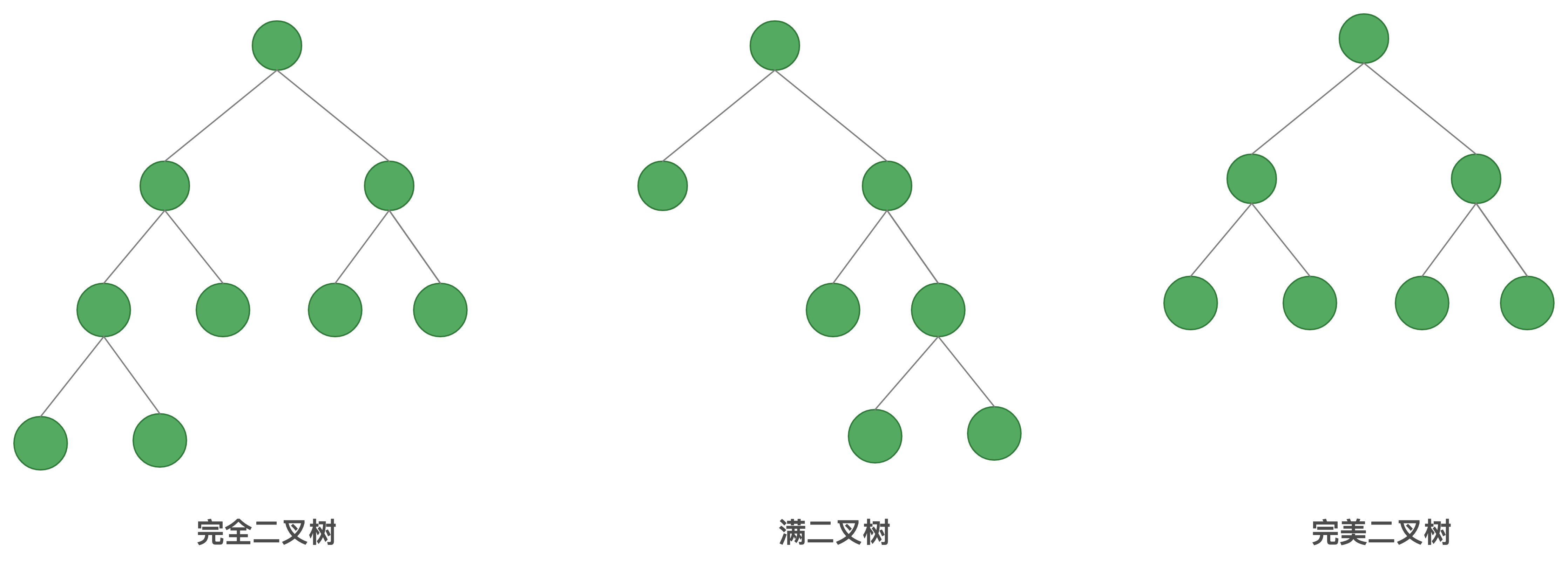
| 完全二叉树 | 除了最后一层的右边,其他节点都已经填满 |
| 满二叉树 | 每个节点有零或者两个子节点 |
| 完美二叉树 | 所有节点都被填满 |
| 类型 | 例子 |
|---|---|
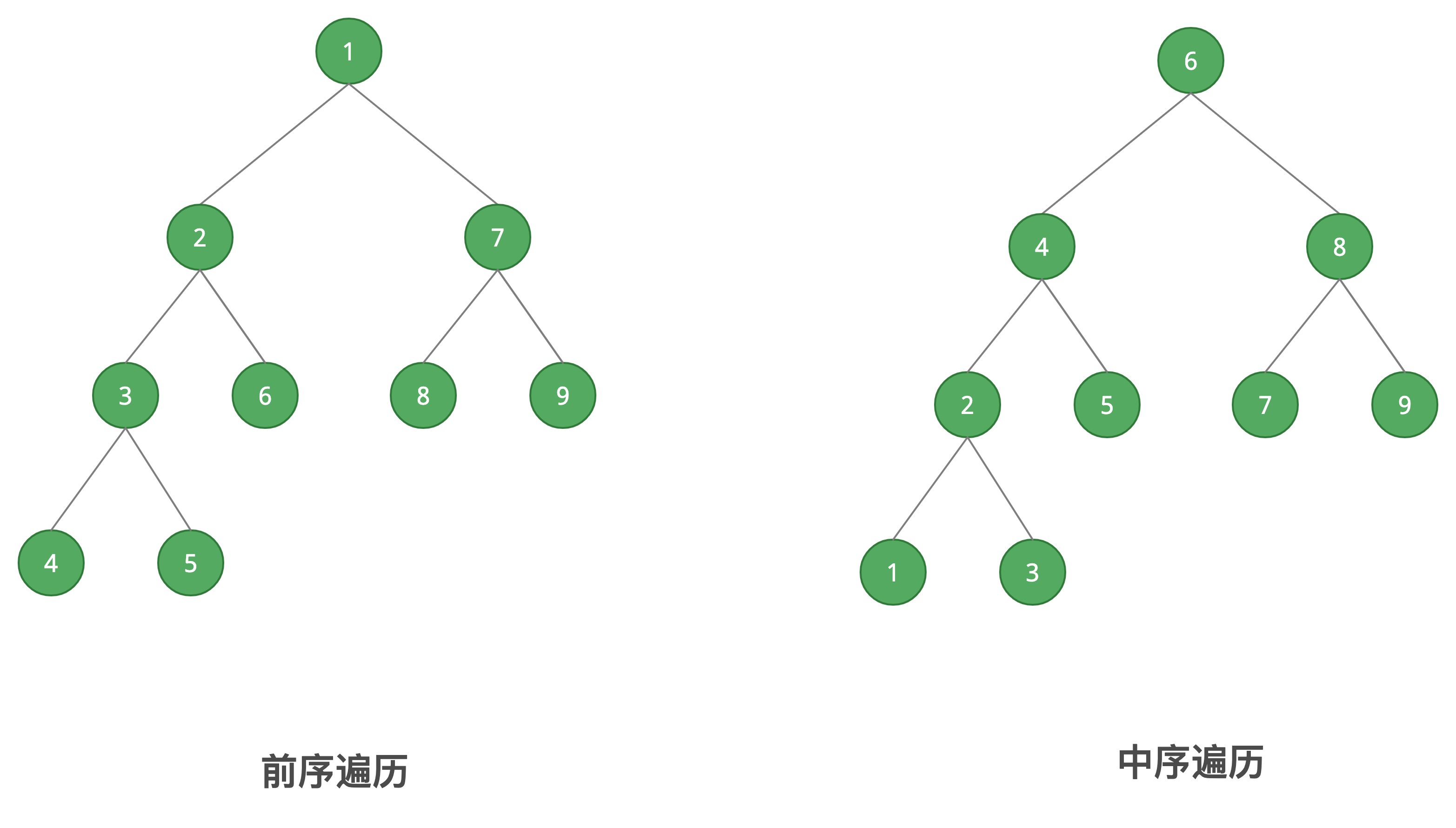
| 前序遍历 | 父节点 -> 左节点 -> 右节点 |
| 中序遍历 | 左节点 -> 父节点 -> 右节点 |
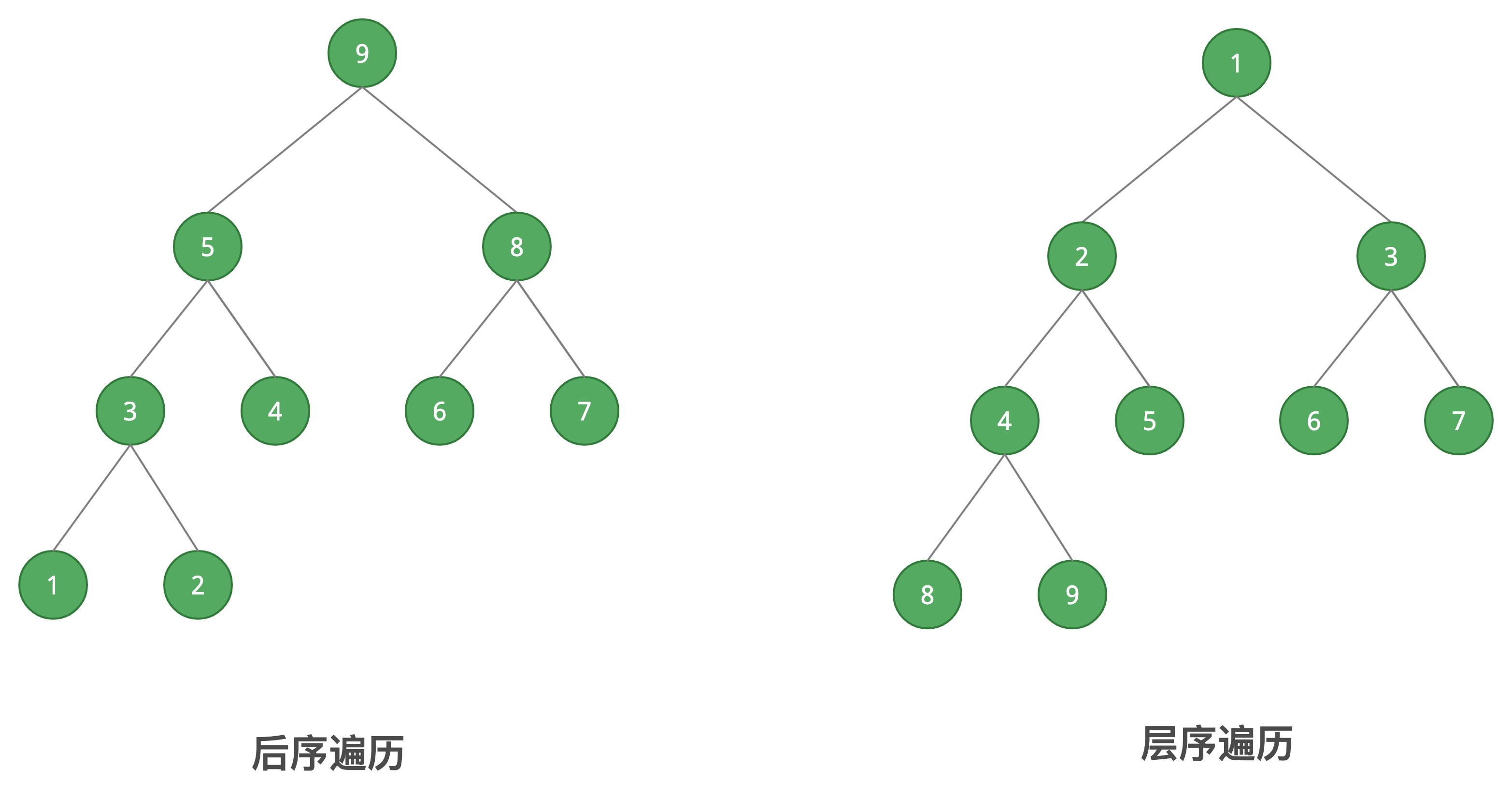
| 后序遍历 | 左节点 -> 右节点 -> 父节点 |
| 层序遍历 | 第一层 -> 第二层 -> 第三层 |
| 问题类型 | 算法 | 要求 | 时间复杂度 |
|---|---|---|---|
| 判断无向图是否有环 |
|
- | O(E+V) |
| 判断有向图是否有环 | - | - | - |
| 无向图最短路径 | - | - | - |
| 有向图最短路径 | - | - | - |
| 所有结点对最短路径 | - | - | - |
| 最小生成树 | - | - | - |
| 强连通分量 | - | - | - |
| 拓扑排序 | - | - | - |